Anomaly detection for low volume metrics

This blog post is the first in a series about our quest to find the best anomaly detection system for chatbots. Our quest is by no means over, but we’ll update you on the problems we tackle as we progress on our journey.

Most of the time-series anomaly or outlier detection algorithms out there, commercial or otherwise, only function well under high volumes of traffic. One of the services Sinch offers is routing phone calls for ride-hailing companies between the driver and the passenger without the need to share their actual phone numbers.

Every customer has a different profile, such as connection success rate and call duration. Performance issues or connection problems can occur for only one customer in only one country. That means that if we want to deliver the best possible service to all of our customers, it’s necessary to monitor a lot of metrics. And for some clients and/or countries, there isn’t always that much traffic.

Dealing with real-world data you often get low traffic metrics that are very noisy. If you take the call success rate, for example, one failed call can skew the data so much that it triggers the anomaly detection system; or makes the data so noisy so it becomes too noisy to model. Take, for example, the traffic illustrated below.

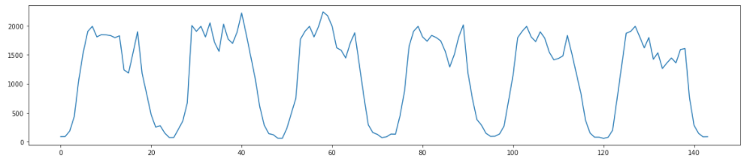
Here we see the number of calls recorded for each hour over six days, with clear peaks during the day and barely any traffic at night. If we show the average call success rate for this traffic, you get something like the image below.

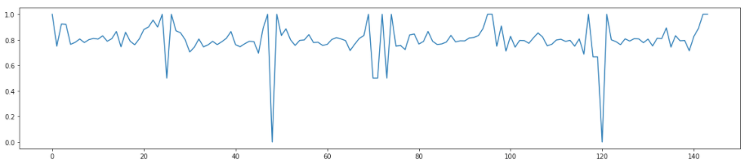
As you can see, the success rate is now all over the place. It ranges between 0 and 1, with 0 being no successful calls in a certain period and 1 with all calls being successful. These spikes typically occur during periods with low traffic at night.

If you look at this data, you see that it can be difficult to set up an anomaly detection system. Every success rate between 0 and 1 seems realistic, so there is no specific success rate that could trigger an anomaly.

One way to avoid this would be to ignore low traffic periods at night. But obviously, anomalies may occur at night. Ignoring this would mean you are flying blind at night. Let’s dive into two methods to convert this noisy metric into something that is much more useful for anomaly detection.

A simple approach to make sure the data you look at is relevant would be to work with a moving average. You can replace each measurement with the average of its past 200 measurements, for example. If you do that for the data illustrated above, you get the green line illustrated below.

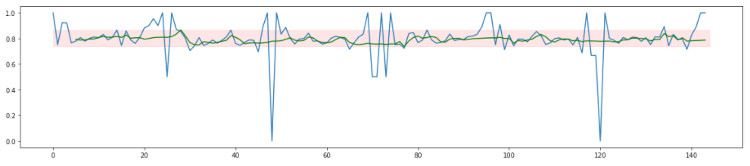
As you can see in the image above, the improved success rate stays nicely between 0.7 and 0.9 and is significantly more stable than the raw data. That approach only requires you to keep data for the past 200 calls in memory.

If you work in a streaming architecture and want to reduce the memory requirements even further, you can work with a first-order (infinite response) low pass filter. That allows you to compute your metric every time a call takes place. If you have a forgetting factor of 0.99 you can compute your next value as follows:

next_value = 0.99 * previous_value + 0.01 * current_success

Here the current_success is respectively 1 or 0 if the most recent call was a success or if it failed. If you apply this to the data illustrated above, you get the following.

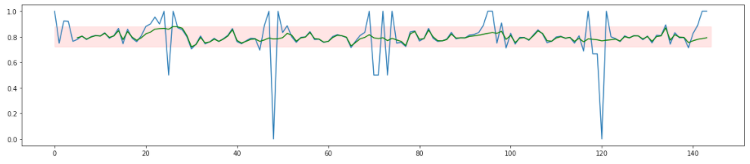
As you can see, once again, we get a smoother graph that stays nicely between 0.7 and 0.9. If you use this as a metric to do anomaly detection, detecting anomalies becomes much easier. You could apply a fixed threshold that triggers an alarm if the average success rate drops below 70%, for example.

Since call monitoring is applied in a real-time setting, the latency before you can detect an anomaly or outlier is really important. The average success rate in this example is 80%. If the success rate drops to 20%, it will take on average 20 calls before noticing this drop with a threshold set at 70%. If there is only a small drop in quality to a 60% success rate, it takes about 70 calls before noticing.

If you want to catch anomalies that span less than, for example, 20 calls, you can use a smaller forgetting factor. For short-lasting anomalies, you can apply a forgetting factor of 0.9 (or a window length of 20 calls), for example.

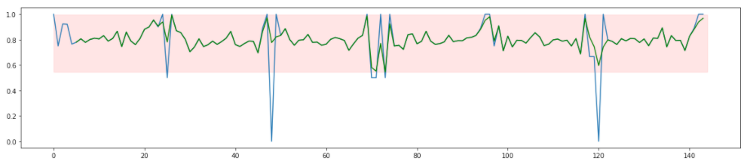
As you can see, this data is much noisier but not as noisy as the original. And because of a forgetting factor of only 0.9, it will take much less time before actual anomalies are detected. Whenever the average success rate drops below 50%, you can trigger an alarm. Using this setting, you can detect a drop to a 20% success rate after seven calls on average. But you might never detect a drop to 60% since your threshold is set to 50%.

To get a good functioning anomaly detection algorithm, you need to monitor over multiple window lengths or forgetting factors. We suggest increasing or decreasing these exponentially. For window lengths, you could use 10, 100, 1000, … or if you want it more fine-grained you can stick to 10, 20, 50, 100, 200, 500, 1000, 2000, … Similarly, you can apply the same logic to the forgetting factors for example 0.9, 0.99, 0.999, … or finer-grained 0.9, 0.95, 0.98, 0.99, 0.995, …

The advantage of this approach is its simplicity. It can turn the metric you measure into a computed metric where each data point is inherently relevant with regards to a corresponding number of calls. Additionally, you can sample this metric at fixed time intervals so that you can use it as an input to many of the existing anomaly detection algorithms or as training data for machine learning methods. Or, if you use one of the commercial infrastructure or application monitoring software packages or tools like Datadog or Dynatrace, you can use this as the input metrics for their anomaly monitor.

The disadvantage of moving averages is that you don’t know beforehand how much time each data point encapsulates. During times of low traffic, your averaging window can span multiple hours, while during peak traffic, it might only be influenced by a couple of minutes of data. Because there is no guarantee that these window widths are the same for each day, it’s hard to model seasonal data using this approach. For seasonal data, we suggest using the time warping approach.

Imagine your call success rate depends on the time of day. During the day time, you can expect 80% of calls to be successful, but after office hours, that success rate drops to 60%, and at night time, you only have 40% successful calls. With the traffic shown in the first graph, you could get the following measured success rate in blue below.

As shown above, the success rate can wildly oscillate between 0 and 1. Instead of using a low pass filter, you can arrange the data in buckets of the same size for each day. If you require at least 200 calls, for example, you get the beginning and end times for the buckets shown in black in the image above. If you apply these buckets to the data shown above and you compute the average success rates, you get the green line shown below.

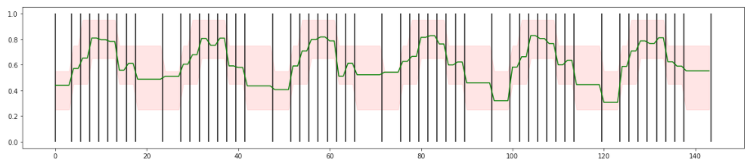
The green line is more stable than the blue line. We can now set boundaries for call success rate at every point during the day shown in red above. Even though the original data was quite noisy, this approach allows us to embed seasonality into the anomaly detection model.

Similar to the example shown above, picking a fixed number of calls within one bucket poses the disadvantage of increased time until an anomaly is detected. But you can aggregate the calls in smaller buckets. Below you can see an example of the calls being clustered by at least 20 calls per bucket.

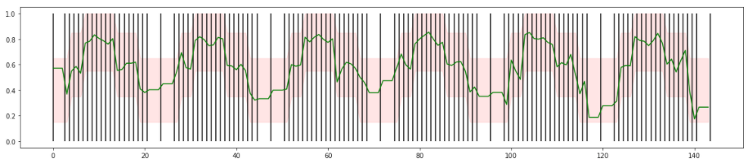
As you can see, the green line is less stable than above, and the boundaries are significantly bigger, but now you will see a deviation happening much faster. Similar to before, you aggregate the data in multiple bucket sizes, covering a broad range to get the best performance. That allows you to spot both big deviations lasting a short amount of time and small deviations over longer periods.

If you compute the time-warped bucket sizes every time a new data point comes in or on a fixed time interval – for example, every minute – you will be able to monitor your time-series with an anomaly detection method that takes seasonality into account.

For non-seasonal data, you can use a moving average approach to convert your metric into something more insightful. Picking a window size that is big enough, you can guarantee that the data you look at is relevant since it inherently will incorporate the number of calls. The resulting metric can be used as input by anomaly detection algorithms requiring stable input.

When you want to take seasonal data into account, we introduced a time-warping method. It guarantees that you have relevant data points, and at the same time, still allows you to model the seasonality of the data.

Although we used phone calls in the blog post, you can use other metrics to ensure that the data points you input into the anomaly detection algorithm are relevant. Think about the number of API calls, messages sent, users logged in, clicks, …

In the next blog post, we’ll cover a couple of the methods we tried to determine the boundaries automatically for an anomaly detection system.

Want to find out more about chatbot technology and how it can help your business? Take a look at the Chatlayer product page here.